高等数学·4 向量代数和空间解析几何
考纲内容
向量的概念
- 向量的线性运算
- 向量的数量积和向量积
- 向量的混合积
- 两向量垂直、平行的条件
- 两向量的夹角
- 向量的坐标表达式及其运算
- 单位向量
- 方向数与方向余弦
曲面方程和空间曲线方程的概念
- 平面方程
- 直线方程
- 平面与平面
- 平面与直线
- 直线与直线的夹角以及平行、垂直的条件
- 点到平面和点到直线的距离
- 球面,柱面,旋转曲面
- 常用的二次曲面方程及其图形
- 空间曲线的参数方程和一般方程
- 空间曲线在坐标面上的投影曲线方程
一、向量及其线性运算
考纲摘要:
- 理解空间直角坐标系,理解向量的概念及其表示
- 理解单位向量、方向数与方向余弦、向量的坐标表达式,掌握用坐标表达式进行向量运算的方法
平行四边形法则等,已是高中熟悉的知识,此处不再赘述
二、数量积 向量积 混合积
考纲摘要:掌握向量的运算(线性运算、数量积、向量积、混合积),了解两个向量垂直、平行的条件
0x00 数量积
已是高中熟悉的知识,此处不再赘述
0x01 向量积
设
被就是向量积。设
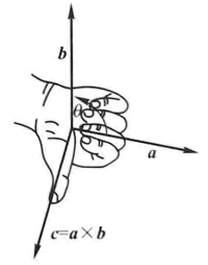
向量积的性质:
- 分配律:
- 与数乘的结合律:
0x02 混合积
先将两向量
假设
混合积的绝对值表示以这三个向量为棱的平行六面体的体积,三个向量共面的充要条件是混合积为 0
三、平面及其方程
考纲摘要:
- 掌握平面方程和直线方程及其求法
- 会求平面与平面、平面与直线、直线与直线之间的夹角,并会利用平面、直线的相互关系(平行、垂直、相交等))解决有关问题
- 会求点到直线以及点到平面的距离
0x00 曲面方程与空间曲线方程的概念
如果曲面
- 曲面
- 不在曲面
那么方程
而空间曲线可以看作是两个曲面的交线,曲线的方程可以写为:
曲线
0x01 平面的点法式方程
如果一个非零向量与一个平面垂直,那么这个向量就叫做这个平面的法线向量,易知,平面上任意一点都和法线向量垂直。 这样一来,知道平面上的一个点与这个平面的其中一个法线向量,就可以完全确定这个平面了。
设
因为
也就有:
这就是一个平面上的任意一点
0x02 平面的一般方程
任何平面都可以用三元一次方程
一些特殊的三元一次方程的图形特点:
同理,
截距式方程:
0x03 两平面的夹角
两个平面的法线向量的夹角(通常指锐角或直角),称为两平面的夹角
设两个平面的方程为:
0x04 点到平面的距离公式
点
四、空间直线及其方程
考纲摘要:
- 掌握平面方程和直线方程及其求法
- 会求平面与平面、平面与直线、直线与直线之间的夹角,并会利用平面、直线的相互关系(平行、垂直、相交等))解决有关问题
- 会求点到直线以及点到平面的距离
0x00 空间直线的方程
1. 空间直线的一般方程
系数矩阵的秩必须为 2,否则就意味着两个平面是平行的,无法确定一条唯一的直线。
2. 空间直线的对称式方程
平行于直线
这样确定出的
这样的方程称作直线的对称式方程或点向式方程
考虑
中含有 0 的情形:
- 当
时,方程组实际上是 - 当
时,实际上这就是一个和 轴平行的直线,方程组为
3. 空间直线的参数方程
对称式方程可以直接导出直线的参数方程:
0x01 两直线的夹角
直接根据数量积的定义求两直线的方向向量的夹角即可,注意方向向量的方向,两直线的夹角要取锐角或者钝角
0x02 直线与平面的夹角
设直线与平面的夹角为
五、曲面及其方程
考纲摘要:
- 了解曲面方程和空间曲线方程的概念
- 了解常用二次曲面的方程及其图形,会求简单的柱面和旋转曲面的方程
0x00 曲面方程的概念
定义:如果曲面
- 曲面
- 不在曲面
那么这个方程
在空间解析几何中,关于曲面的研究有以下两个基本问题:
- 已知一曲面作为点的几何轨迹时,建立这个曲面的方程
- 已知坐标
间的一个方程时,研究这个方程所表示的曲面的形状
0x01 旋转曲面
定义:一条平面曲线绕其平面上一条定直线旋转一周形成的曲面叫做旋转曲面,该定直线称为轴,这条曲线称为母线
给定
0x02 柱面
定义:平行定直线并沿着定曲线
0x03 二次曲面
把三元二次方程
其基本类型有:椭球面、抛物面、双曲面、锥面 研究二次曲面特性的基本方法:截痕法
1. 椭球面
与坐标面的交线是椭圆
截痕:与
当
2. 抛物面
椭圆抛物面
特别的,当
双曲抛物面(鞍型曲面)
注意,以上
3. 双曲面
单叶双曲面
平面
平面
双叶双曲面
4. 椭圆锥面
六、空间曲线及其方程
考纲摘要:
- 了解曲面方程和空间曲线方程的概念
- 了解空间曲线的参数方程和一般方程,了解空间曲线在坐标平面上的投影,并会求该投影曲线的方程
0x00 空间曲线的一般方程
空间曲线可以视作两个曲面的交线,其一般方程为:
0x01 空间曲线的参数方程
0x02 空间曲线在坐标面上的投影
假设空间曲线
那么方程:
表示的曲线必定包含空间曲线
本章公式汇总
本章公式:
平面的点法式方程
平面的一般方程
平面的截距式方程
平面夹角余弦值:
点到平面的距离公式: