高等数学·6 多元函数积分学 PART.1 重积分

考纲内容

• 二重积分与三重积分的概念、性质、计算和应用
• 两类曲线积分的概念、性质及计算
• 两类曲线积分的关系
• 格林（Green）公式
• 平面曲线积分与路径无关的条件
• 二元函数全微分的原函数
• 两类曲面积分的概念、性质及计算
• 两类曲面积分的关系
• 高斯（Gauss）公式
• 斯托克斯（Stokes）公式
• 散度、旋度的概念及计算
• 曲线积分和曲面积分的应用

一、二重积分的概念与性质

考纲摘要：理解二重积分的概念

0x00 二重积分的定义

考纲摘要：理解二重积分的概念

设 $f(x,y)$$f(x,y)$ 是有界闭区域 $D$$D$ 上的有界函数， 将闭区域 $D$$D$ 任意分为 $n$$n$ 个小闭区域：$\mathrm{\Delta }{\sigma }_1,\mathrm{\Delta }{\sigma }_2,\dots ,\mathrm{\Delta }{\sigma }_n$$\Delta\sigma_1,\Delta\sigma_2,\dots,\Delta\sigma_n$

其中 $\mathrm{\Delta }{\sigma }_i$$\Delta\sigma_i$ 表示第 $i$$i$ 个小闭区域，亦表示其面积。 在其上任取一点 $({\xi }_i,{\eta }_i)$$(\xi_i,\eta_i)$，做乘积并作和 $\sum _{i=1}^{n}f({\xi }_i,{\eta }_i)\mathrm{\Delta }{\sigma }_i$$\sum_{i=1}^{n}f(\xi_i,\eta_i)\Delta\sigma_i$

如果当各个小闭区域的直径中最大值 $\lambda \to 0$$\lambda\to 0$ 时，这个和式的极限总存在， 且与闭区域 $D$$D$ 的分法及 $({\xi }_i,{\eta }_i)$$(\xi_i,\eta_i)$ 的取法无关 那么称此时的极限为函数 $f(x,y)$$f(x,y)$ 在闭区域 $D$$D$ 上的二重积分，记作：

• $f(x,y)$$f(x,y)$ 叫做被积函数
• $f(x,y)\mathrm{d}\sigma$$f(x,y)\mathrm{d}\sigma$ 叫做被积表达式
• $\mathrm{d}\sigma$$\mathrm{d}\sigma$ 叫做面积元素
• $x$$x$ 和 $y$$y$ 叫做积分变量
• $D$$D$ 叫做积分区域
• $\sum _{i=1}^{n}f({\xi }_i,{\eta }_i)\mathrm{\Delta }{\sigma }_i$$\sum_{i=1}^{n}f(\xi_i,\eta_i)\Delta\sigma_i$叫做积分和

如果 $\mathrm{\Delta }{\sigma }_i$$\Delta\sigma_i$ 是矩形闭区域且边长为 $\mathrm{\Delta }{x}_i$$\Delta x_i$ 和 $\mathrm{\Delta }{y}_i$$\Delta y_i$，那么 $\mathrm{d}\sigma$$\mathrm{d}\sigma$ 也可以记作 $\mathrm{d}x\mathrm{d}y$$\mathrm{d}x\mathrm{d}y$，二重积分就记作：

$\mathrm{d}x\mathrm{d}y$$\mathrm{d}x\mathrm{d}y$叫做直角坐标系中的面积元素

0x01 二重积分的性质

考纲摘要：了解重积分的性质

1. 二重积分常系数的处理

假设 $\alpha$$\alpha$ 和 $\beta$$\beta$ 都是常数，则有：

2. 二重积分的可加性

如果闭区域 $D$$D$ 可以被有限条曲线分为有限个部分闭区域，那么 $D$$D$ 上的二重积分等于各闭区域上二重积分的和。例如：

假设 $D$$D$ 可以分为两个闭区域 $D_1$$D_1$ 和 $D_2$$D_2$，则有：

3. 高为 1 的平顶柱体的体积

4. 二重积分间的大小关系

如果在 $D$$D$ 上，$f(x,y)\le g(x,y)$$f(x,y)\le g(x,y)$，则有：

由于 $-|f(x,y)|\le f(x,y)\le |f(x,y)|$$-|f(x,y)|\le f(x,y)\le|f(x,y)|$，则：

5. 二重积分的估值

设 $M$$M$ 和 $m$$m$ 分别是 $f(x,y)$$f(x,y)$ 在闭区域 $D$$D$ 上的最大值和最小值，$\sigma$$\sigma$ 是 $D$$D$ 的面积，则有：

6. 二重积分的中值定理

考纲摘要：了解二重积分的中值定理

设函数 $f(x,y)$$f(x,y)$ 在闭区域 $D$$D$ 上连续，$\sigma$$\sigma$ 是 $D$$D$ 的面积，则在 $D$$D$ 上至少存在一点 $(\xi ,\eta )$$(\xi,\eta)$，使得：

二、二重积分的计算

考纲摘要：掌握二重积分的计算方法（直角坐标、极坐标）

0x00 区域 $D$$D$ 的表示

一般而言，区域 $D$$D$ 可以表示为：${\varphi }_1(x)\le y\le {\varphi }_2(x),a\le x\le b$$\phi_1(x)\le y\le\phi_2(x),a\le x\le b$ 能够这样表示的区域被称作 $X$$X$ 型区域 还有 $Y$$Y$ 型区域，可以表示为：${\varphi }_1(y)\le y\le {\varphi }_2(y),a\le y\le b$$\phi_1(y)\le y\le\phi_2(y),a\le y\le b$

显然，例如说对于 $X$$X$ 型区域，其满足平行于 $y$$y$ 轴的直线于这个区域的交点最多只有两个 当然，一个区域并不一定是 $X$$X$ 型区域或者 $Y$$Y$ 型区域，但是可以将其拆分成几个 $X$$X$ 型区域或者 $Y$$Y$ 型区域

0x01 利用直角坐标计算二重积分

考纲摘要：掌握二重积分的计算方法（直角坐标、极坐标）

1. $X$$X$ 型区域的情形

如果 $D$$D$ 可以用 ${\varphi }_1(x)\le y\le {\varphi }_2(x),a\le x\le b$$\phi_1(x)\le y\le\phi_2(x),a\le x\le b$ 表示，那么可以写成以下等式：

也就是说，先把 $x$$x$ 看作常数，求解中括号内的定积分，然后把求解出的结果看作是对 $x$$x$ 的函数，再对这个函数进行定积分，即可求得结果。

此外，以上表达式还可以记作：

2. $Y$$Y$ 型区域的情形

如果 $D$$D$ 可以用 ${\varphi }_1(y)\le x\le {\varphi }_2(y),a\le y\le b$$\phi_1(y)\le x\le\phi_2(y),a\le y\le b$ 表示，那么可以写成以下等式：

也就是说，先把 $y$$y$ 看作常数，求解中括号内的定积分，然后把求解出的结果看作是对 $y$$y$ 的函数，再对这个函数进行定积分，即可求得结果。

此外，以上表达式还可以记作：

如果区域 $D$$D$ 既是 $X$$X$ 型区域又是 $Y$$Y$ 型区域，则按 $X$$X$ 型区域计算的积分与按 $Y$$Y$ 型区域计算的积分相等

例题

计算 $\underset{D}{\iint }x{y}^2\mathrm{d}x\mathrm{d}y$$\iint_\limits{D}xy^2\mathrm dx\mathrm dy$，其中，区域 $D$$D$ 由 $y=x,x+y=1$$y=x,x+y=1$ 及 $x$$x$ 轴围成。

首先让我们画出它的积分区域：

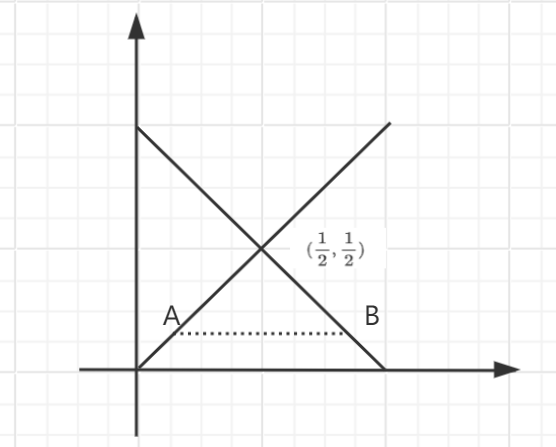
当我们对这个区域任意做一个与 $x$$x$ 轴平行的直线时，它与区域的边界分别交于 $A,B$$A,B$ 点 它们的纵坐标都是 $y$$y$，因此 $A(y,y),B(1-y,y)$$A(y,y),B(1-y,y)$，因此积分式就可以写成：

$${\int }_0^{\frac{1}{2}}\mathrm{d}y{\int }_y^{1-y}x{y}^2\mathrm{d}x$$

而这就是一个 $Y$$Y$ 型区域的积分。因此，确认积分上下限其实很简单，甚至无需取寻找一个 ${\varphi }_1(y)<x<{\varphi }_2(y)$$\phi_1(y)<x<\phi_2(y)$，只需做这样的与坐标轴平行的直线，然后用另一个坐标轴的变量表示出这条直线与边界的交点即可。

接下来让我们来计算这个积分：

$$\begin{array}{c}{\int }_y^{1-y}x{y}^2\mathrm{d}x=\frac{1}{2}{x}^2{y}^2{|}_y^{1-y}=\frac{1}{2}{y}^2[(1-y{)}^2-y^2]=\frac{1}{2}{y}^2-y^3\\ {\int }_0^{\frac{1}{2}}\mathrm{d}y{\int }_y^{1-y}x{y}^2\mathrm{d}x={\int }_0^{\frac{1}{2}}(\frac{1}{2}{y}^2-y^3)\mathrm{d}y=\frac{1}{6}{y}^3-\frac{1}{4}{y}^4{|}_0^{\frac{1}{2}}=\frac{1}{192}\end{array}$$

0x02 利用极坐标计算二重积分

考纲摘要：掌握二重积分的计算方法（直角坐标、极坐标）

普通二元函数的二重积分可以化为极坐标形式：

同样可以按照一般的二重积分进行计算：

条件是 ${\varphi }_1(\theta )\le \rho \le {\varphi }_2(\theta ),\alpha \le \theta \le \beta$$\phi_1(\theta)\le\rho\le\phi_2(\theta),\alpha\le\theta\le\beta$

*0x03 二重积分的换元法

设 $f(x,y)$$f(x,y)$ 是在 $xOy$$xOy$ 平面上的闭区域 $D$$D$ 上连续，若变换：$T:x=x(u,v),y=y(u,v)$$T:x=x(u,v),y=y(u,v)$

将 $uOv$$uOv$ 平面上的闭区域 $D^{\prime }$$D'$ 变为 $xOy$$xOy$ 平面上的 $D$$D$ ,且满足

• $x(u,v),y(u,v)$$x(u,v),y(u,v)$在 $D^{\prime }$$D'$ 上具有一阶连续偏导数

• 在 $D^{\prime }$$D'$ 上的雅可比式：

  $$\begin{array}{c}J(u,v)=\frac{\partial (x,y)}{\partial (u,v)}=\left|\begin{array}{cc}\frac{\partial x}{\partial u}& \frac{\partial x}{\partial v}\\ \frac{\partial y}{\partial u}& \frac{\partial y}{\partial v}\end{array}\right|\ne \end{array}$$

• 变换 $T:D^{\prime }\to D$$T:D'\to D$ 是一对一的，则有：

  $$\underset{D}{\iint }f(x,y)\mathrm{d}x\mathrm{d}y=\underset{D^{\prime }}{\iint }f[x(u,v),y(u,v)]|J(u,v)|\mathrm{d}u\mathrm{d}v$$

  这就是二重积分的换元公式

四、三重积分

考纲摘要：理解三重积分的概念

0x00 三重积分的概念

设 $f(x,y,z)$$f(x,y,z)$ 是空间有界闭区域 $\mathrm{\Omega }$$\Omega$ 上的有界函数，将 $\mathrm{\Omega }$$\Omega$ 任意分为 $n$$n$ 个小闭区域 $\mathrm{\Delta }{v}_1,\mathrm{\Delta }{v}_2,\dots ,\mathrm{\Delta }{v}_n$$\Delta v_1,\Delta v_2,\dots,\Delta v_n$

其中 $\mathrm{\Delta }{v}_i$$\Delta v_i$ 表示第 $i$$i$ 个小闭区域，也表示其体积。 在每个 $\mathrm{\Delta }{v}_i$$\Delta v_i$ 上任取一点 $({\xi }_i,{\eta }_i,{\zeta }_i)$$(\xi_i,\eta_i,\zeta_i)$，作乘积 $f({\xi }_i,{\eta }_i,{\zeta }_i)\mathrm{\Delta }{v}_i,i=1,2,\dots ,n$$f(\xi_i,\eta_i,\zeta_i)\Delta v_i,i=1,2,\dots,n$ ，并作和 $\sum _{i=1}^{n}f({\xi }_i,{\eta }_i,{\zeta }_i)\mathrm{\Delta }{v}_i$$\sum_{i=1}^nf(\xi_i,\eta_i,\zeta_i)\Delta v_i$ 如果各个小闭区域 $\lambda \to 0$$\lambda\to0$ 时，这个和的极限总存在，且与闭区域 $\mathrm{\Omega }$$\Omega$ 的分发及点 $({\xi }_i,{\eta }_i,{\zeta }_i)$$(\xi_i,\eta_i,\zeta_i)$ 的取法无关 那么称此极限为函数 $f(x,y,z)$$f(x,y,z)$ 在闭区域 $\mathrm{\Omega }$$\Omega$ 上的三重积分，记作 $\underset{\mathrm{\Omega }}{\iiint }f(x,y,z)\mathrm{d}v$$\iiint_\limits{\Omega}f(x,y,z)\mathrm{d}v$，也就是：

其中，$f(x,y,z)$$f(x,y,z)$ 叫做被积函数，$\mathrm{d}v$$\mathrm{d}v$ 叫做体积元素，$\mathrm{\Omega }$$\Omega$ 叫做积分区域

0x01 三重积分的计算

考纲摘要：会计算三重积分（直角坐标、柱面坐标、球面坐标）

计算三重积分可以把它转换成积分三次。以下是把三重积分化为积分三次的方法

1. 利用直角坐标计算三重积分

考纲摘要：会计算三重积分（直角坐标）

设区域 $\mathrm{\Omega }$$\Omega$ 的两个边界曲面为：

此时，积分区域 $\mathrm{\Omega }$$\Omega$ 可以表示为： $\mathrm{\Omega }=\{(x,y,z)|z_1(x,y)\le z\le z_2(x,y),(x,y)\in D_{xy}\}$$\Omega=\{(x,y,z)|z_1(x,y)\le z\le z_2(x,y),(x,y)\in D_{xy}\}$

这样，先把 $f(x,y,z)$$f(x,y,z)$ 看作 $z$$z$ 的函数，然后对区间 $[z_1(x,y),z_2(x,y)]$$[z_1(x,y),z_2(x,y)]$ 进行积分，会得到一个二元函数 $F(x,y)$$F(x,y)$

然后计算 $F(x,y)$$F(x,y)$ 在闭区域 $D_{xy}$$D_{xy}$ 上的二重积分即可。最终的计算公式为：

$\mathrm{\Omega }=\{(x,y,z)|z_1(x,y)\le z\le z_2(x,y),(x,y)\in D_{xy}\}$$\Omega=\{(x,y,z)|z_1(x,y)\le z\le z_2(x,y),(x,y)\in D_{xy}\}$

$D_{xy}=\{(x,y)|y_1(x)\le y\le y_2(x),a\le x\le b\}$$D_{xy}=\{(x,y)|y_1(x)\le y\le y_2(x),a\le x\le b\}$

2. 利用柱面坐标计算三重积分

考纲摘要：会计算三重积分（柱面坐标）

(1) 柱面坐标的概念

设点 $M(x,y,z)$$M(x,y,z)$ 设 $M$$M$ 在 $xOy$$xOy$ 面上的投影 $P$$P$ 的极坐标为 $\rho ,\theta$$\rho,\theta$

则 $\rho ,\theta ,z$$\rho,\theta,z$ 叫做 $M$$M$ 的柱面坐标

与直角坐标的关系：

(2) 计算三重积分

体积元素：$\mathrm{d}v=\rho \mathrm{d}\rho \mathrm{d}\theta \mathrm{d}z$$\mathrm{d}v=\rho\mathrm d\rho\mathrm d\theta\mathrm dz$

有以下关系：

注意：需要界定 $\rho ,\theta ,z$$\rho,\theta,z$ 的范围

3. 利用球面坐标计算三重积分

考纲摘要：会计算三重积分（球面坐标）

(1) 球面坐标

设 $M(x,y,z)$$M(x,y,z)$ 是空间内一点，那么 $M$$M$ 也可以用这样三个有次序的数 $r,\varphi ,\theta$$r,\phi,\theta$ 来确定。

• $r$$r$ 是原点 $O$$O$ 到点 $M$$M$ 的距离
• $\varphi$$\phi$ 是向量 $\overrightarrow{OM}$$\overrightarrow{OM}$ 与 $z$$z$ 轴正向的夹角
• $\theta$$\theta$ 是向量 $\overrightarrow{OP}$$\overrightarrow{OP}$与 $x$$x$ 轴正向的夹角，$P$$P$ 是 $M$$M$ 在 $xOy$$xOy$ 面的投影

直角坐标与其对应的球面坐标的关系：

(2) 计算三重积分

体积元素：$\mathrm{d}v=r^2\sin \varphi \mathrm{d}r\mathrm{d}\varphi \mathrm{d}\theta$$\mathrm dv=r^2\sin\phi\mathrm dr\mathrm d\phi\mathrm d\theta$

有以下关系：

当然，需要界定 $r,\varphi ,\theta$$r,\phi,\theta$ 的范围

五、重积分的应用

0x00 曲面的面积

如果曲面 $S$$S$ 由方程 $z=f(x,y)$$z=f(x,y)$ 确定，要求其在闭区域 $D$$D$ 下的面积 $A$$A$

其面积元素为：

推导出曲面面积的计算公式：

曲面由参数方程确立的情形

需要满足

不全为零，则曲面 $S$$S$ 的面积为：

其中，

助记：观察 $E,F,G$$E,F,G$ 各自的特点，很容易就能记住。

0x01 质心

设平面薄片上有 $n$$n$ 个点，其坐标分别为 $(x_1,y_1),(x_2,y_2),\dots ,(x_n,y_n)$$(x_1,y_1),(x_2,y_2),\dots,(x_n,y_n)$

则其质心坐标为：

设其在点 $(x,y)$$(x,y)$ 的密度为 $\mu (x,y)$$\mu(x,y)$，则：

同样地，对于一个物体，其质心也可以这样求：

0x02 转动惯量

设平面薄片上有 $n$$n$ 个质点，其坐标分别为$(x_1,y_1),(x_2,y_2),\dots ,(x_n,y_n)$$(x_1,y_1), (x_2,y_2),\dots,(x_n,y_n)$，质量分别为 $m_1,m_2,\dots ,m_n$$m_1,m_2,\dots,m_n$

那么，这个质点系对 $x$$x$ 轴与对 $y$$y$ 轴的转动惯量分别为：

设点 $(x,y)$$(x,y)$ 处的指点的密度为 $\mu (x,y)$$\mu(x,y)$，那么有：

同样的，对于一个物体，其对 $x$$x$ 轴，$y$$y$ 轴，$z$$z$ 轴的转动惯量为：

0x03 引力

空间一物体对某一质点 $P_0(x_0,y_0,z_0)$$P_0(x_0,y_0,z_0)$ 处单位质量的质点的引力 设这个物体在 $(x,y,z)$$(x,y,z)$ 处的密度为 $\rho (x,y,z)$$\rho(x,y,z)$ 则合力 $F$$F$ 在三个坐标轴上的分量为：