概率论·3 多维随机变量及其分布

考纲内容

• 多维随机变量及其分布
• 二维离散型随机变量的概率分布、边缘分布和条件分布
• 二维连续型随机变量的概率密度、边缘概率密度和条件密度
• 随机变量的独立性和不相关性
• 常用二维随机变量的分布
• 两个及两个以上随机变量简单函数的分布

一、二维随机变量

考纲摘要：理解多维随机变量的概念，理解多维随机变量的分布的概念和性质

0x00 二维随机变量及其分布函数

设 $E$$E$ 是一个随机试验，它的样本空间为 $S=\{e\}$$S=\{e\}$，设 $X=X(e),Y=Y(e)$$X=X(e),Y=Y(e)$ 是定义在 $S$$S$ 上的随机变量 由它们构成的一个向量 $(X,Y)$$(X,Y)$ 叫做二维随机变量

称作二维随机变量 $(X,Y)$$(X,Y)$ 的分布函数，也称作随机变量 $X,Y$$X,Y$ 的联合分布函数

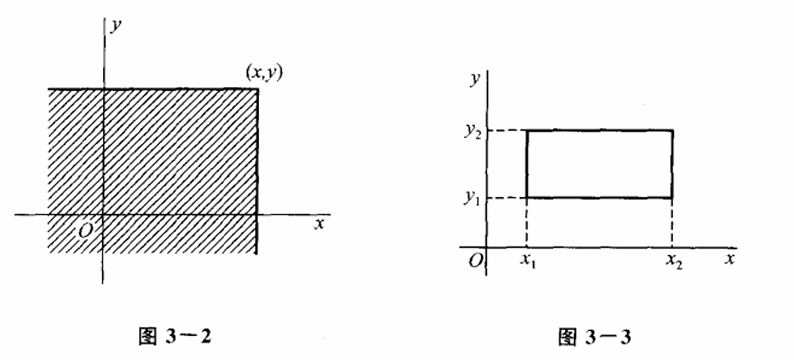
$F(x,y)$$F(x,y)$ 可以看作是平面上的点落在图 3-2 区域上的概率 而落在矩形域 $\{(x,y)|x_1<x\le x_2.y_1<y\le y_2\}$$\{(x,y)|x_1<x\le x_2.y_1< y\le y_2\}$ 的概率为： $P\{x_1<X\le x_2,y_1<Y\le y_2\}=F(x_2,y_2)-F(x_2,y_1)+F(x_1,y_1)-F(x_1,y_2)$$P\{x_1<X\le x_2,y_1<Y\le y_2\}=F(x_2,y_2)-F(x_2,y_1)+F(x_1,y_1)-F(x_1,y_2)$

分布函数 $F(x,y)$$F(x,y)$ 的具有如下性质：

• $F(x,y)$$F(x,y)$ 是变量 $x,y$$x,y$ 的不减函数，即 对于任意固定的 $y$$y$，当 $x_2>x_1$$x_2>x_1$ 时 $F(x_2,y)\ge F(x_1,y)$$F(x_2,y)\ge F(x_1,y)$ 对于任意固定的 $x$$x$，当 $y_2>y_1$$y_2>y_1$ 时 $F(x,y_2)\ge F(x,y_1)$$F(x,y_2)≥F(x,y_1)$
• $0\le F(x,y)\le 1$$0\le F(x,y)\le1$，且 对于任意固定的 $y$$y$，$F(-\mathrm{\infty }，y)=0$$F(-\infty，y)=0$ 对于任意固定的 $x$$x$ ，$F(x,-\mathrm{\infty })=0$$F(x,-\infty)=0$ $F(-\mathrm{\infty },-\mathrm{\infty })=0,F(\mathrm{\infty },\mathrm{\infty })=1s$$F(-\infty,-\infty)=0,F(\infty,\infty)=1s$
• $\underset{\mathrm{\Delta }x\to 0^{+}}{lim}F(x+\mathrm{\Delta }x,y)=F(x,y),\underset{\mathrm{\Delta }y\to 0^{+}}{lim}F(x,y+\mathrm{\Delta }y)=F(x,y)$$\lim_{\Delta x\to 0^+}F(x+\Delta x,y)=F(x,y),\lim_{\Delta y\to 0^+}F(x,y+\Delta y)=F(x,y)$，也就是它对 $x,y$$x,y$ 均右连续
• $\mathrm{\forall }(x_1,y_1),(x_2,y_2),x_1<x_2,y_1<y_2,F(x_2,y_2)-F(x_2,y_1)+F(x_1,y_1)-F(x_1,y_2)\ge 0$$\forall(x_1,y_1),(x_2,y_2),x_1<x_2,y_1<y_2,F(x_2,y_2)-F(x_2,y_1)+F(x_1,y_1)-F(x_1,y_2)\ge0$

0x01 边缘分布

二维随机变量 $(X,Y)$$(X,Y)$ 作为一个整体，具有分布函数 $F(x,y)$$F(x,y)$ 而 $X,Y$$X,Y$ 都是随机变量，各自也有分布函数，将它们分别记为 $F_X(x),F_Y(y)$$F_X(x),F_Y(y)$，依次称为二维随 机变量 $(X,Y)$$(X,Y)$ 关于 $X$$X$ 和关于 $Y$$Y$ 的边缘分布函数。边缘分布函数可以由 $F(x,y)$$F(x,y)$ 来确定：

二、离散型的二维随机变量

考纲摘要：理解二维离散型随机变量的概率分布、边缘分布和条件分布

0x00 离散型的二维随机变量的概率分布

如果二维随机变量 $(X,Y)$$(X,Y)$ 全部可能取到的值是有限对或可列无限多对，则称 $(X,Y)$$(X,Y)$ 是离散型的随机变量.

设其所有可能取值为 $(x_i,y_j),i,j=1,2,\cdots$$(x_i,y_j),i,j=1,2,\cdots$，记 $P\{X=x_i,Y=y_j\}=p_{ij},i,j=1,2,\cdots$$P\{X=x_i,Y=y_j\}=p_{ij},i,j=1,2,\cdots$，则有：

• $p_{ij}\ge 0$$p_{ij}\ge0$
• $\sum _{i=1}^{\mathrm{\infty }}\sum _{j=1}^{\mathrm{\infty }}{p}_{ij}=1$$\sum_{i=1}^\infty\sum_{j=1}^\infty p_{ij}=1$

其称之为二维随机变量 $(X,Y)$$(X,Y)$ 的分布律，或随机变量 $X,Y$$X,Y$ 的联合分布率，也可以用表格来表示：

0x01 离散型的二维随机变量的边缘分布

对于离散型随机变量，显然有：

也就是说，如果考虑上一节中的表格， 若希望求 $X$$X$ 的边缘分布律，只需将所有行全部相加成一行 若希望求 $Y$$Y$ 的边缘分布律，只需将所有列全部相加成一列

0x02 离散型的条件分布率

设 $(X,Y)$$(X,Y)$ 是二维离散型随机变量，对于固定的 $j$$j$，若 $P\{Y=y_j\}>0$$P\{Y=y_j\}>0$，则：

称为在 $Y=y_j$$Y=y_j$ 条件下随机变量 $X$$X$ 的条件分布律

三、连续型的二维随机变量

考纲摘要：理解二维连续型随机变量的概率密度、边缘密度和条件密度，会求与二维随机变量相关事件的概率

0x00 连续型的二维随机变量的概率密度

考纲摘要：理解二维连续型随机变量的概率密度

对于二维随机变量 $(X,Y)$$(X,Y)$ 的分布函数 $F(x,y)$$F(x,y)$，如果存在非负的函数 $f(x,y)$$f(x,y)$ 使对于任意 $x,y$$x,y$ 有

则称 $(X,Y)$$(X,Y)$ 是连续型的二维随机变量，函数 $f(x,y)$$f(x,y)$ 称为二维随机变量 $(X,Y)$$(X,Y)$ 的概率密度，或称为随机变量 $X,Y$$X,Y$ 的联合概率密度 按定义，概率密度 $f(x,y)$$f(x,y)$ 具有以下性质：

• $f(x,y)\ge 0$$f(x,y)\ge 0$
• ${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}f(x,y)\mathrm{d}x\mathrm{d}y=F(\mathrm{\infty },\mathrm{\infty })=1$$\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x,y)\mathrm dx\mathrm dy=F(\infty,\infty)=1$
• 设 $G$$G$ 是 $xOy$$xOy$ 上的区域，点 $(X,Y)$$(X,Y)$ 落在 $G$$G$ 内的概率为 $P\{(X,Y)\in G\}={\iint }_{G}f(x,y)\mathrm{d}x\mathrm{d}y$$P\{(X,Y)\in G\}=\iint_G f(x,y)\mathrm dx\mathrm dy$（该是第一类二重积分）
• 若 $f(x,y)$$f(x,y)$ 在点 $(x,y)$$(x,y)$ 连续，则有 $\frac{{\partial }^{2}F(x,y)}{\partial x\partial y}=f(x,y)$$\cfrac{\part^2F(x,y)}{\part x\part y}=f(x,y)$

0x01 连续型的二维随机变量的边缘概率密度

考纲摘要：理解二维连续型随机变量的边缘密度

边缘概率密度函数如下：

分别称之为 $(X,Y)$$(X,Y)$ 关于 $X$$X$ 和 $Y$$Y$ 的边缘概率密度

0x02 连续型的条件概率密度

设二维随机变量 $(X,Y)$$(X,Y)$ 的概率密度为 $f(x,y)$$f(x,y)$，$(X,Y)$$(X,Y)$ 关于 $Y$$Y$ 的边缘概率密度为 $f_Y(y)$$f_Y(y)$ 若对于固定的 $y,f_Y(y)>0$$y,f_Y(y)>0$，则称

为在 $Y=y$$Y=y$ 条件下 $X$$X$ 的条件概率密度，称

为在 $Y=y$$Y=y$ 的条件下 $X$$X$ 的条件分布函数

四、相互独立的随机变量

考纲摘要：理解随机变量的独立性及不相关性的概念，掌握随机变量相互独立的条件

设 $F(x,y)$$F(x,y)$ 及 $F_X(x),F_Y(y)$$F_X(x),F_Y(y)$ 分别是二维随机变量 $(X,Y)$$(X,Y)$ 的分布函数及边缘分布函数，若

也就是 $F(x,y)=F_X(x)F_Y(y)$$F(x,y)=F_X(x)F_Y(y)$，则称随机变量 $X$$X$ 和 $Y$$Y$ 是相互独立的。

如果 $(X,Y)$$(X,Y)$ 是连续型随机变量，则 $X,Y$$X,Y$ 相互独立的条件等价于 $f(x,y)=f_X(x)f_Y(y)$$f(x,y)=f_X(x)f_Y(y)$

设 $(X_1,X_2,\cdots ,X_m),(Y_1,Y_2,\cdots ,Y_n)$$(X_1,X_2,\cdots,X_m),(Y_1,Y_2,\cdots,Y_n)$ 相互独立，则 $X_i,Y_j,i=1,2,\cdots ,m,j=1,2,\cdots ,n$$X_i,Y_j,i=1,2,\cdots,m,j=1,2,\cdots,n$ 相互独立。 如果 $h,g$$h,g$ 是连续函数，则 $h(X_1,X_2,\cdots ,X_m),g(Y_1,Y_2,\cdots ,Y_n)$$h(X_1,X_2,\cdots,X_m),g(Y_1,Y_2,\cdots,Y_n)$ 相互独立

五、随机变量的函数的分布

考纲摘要：会求两个随机变量简单函数的分布，会求多个相互独立随机变量简单函数的分布

0x00 $Z=X+Y$$Z=X+Y$ 的分布

设 $(X,Y)$$(X,Y)$ 是二维连续型随机变量，它具有概率密度 $f(x,y)$$f(x,y)$，则 $Z=X+Y$$Z=X+Y$ 仍为连续型随机变量，其概率密度为：

如果 $X,Y$$X,Y$ 相互独立，则：

这称为 $f_X,f_Y$$f_X,f_Y$ 的卷积公式，记作 $f_X\ast f_Y$$f_X*f_Y$

正态分布的情形

设 $X,Y$$X,Y$ 相互独立且 $X\sim N({\mu }_1,{\sigma }_1^2),Y\sim N({\mu }_2,{\sigma }_2^2)$$X\sim N(\mu_1,\sigma_1^2),Y\sim N(\mu_2,\sigma_2^2)$ 则 $Z=X+Y$$Z=X+Y$ 服从正态分布，且 $Z\sim N({\mu }_1+{\mu }_2,{\sigma }_1^2+{\sigma }_2^2)$$Z\sim N(\mu_1+\mu_2,\sigma_1^2+\sigma_2^2)$

也可以推广到 $N$$N$ 个独立正态随机变量 $X_i\sim N({\mu }_i,{\sigma }_i^2),i=1,2,\cdots ,n$$X_i\sim N(\mu_i,\sigma_i^2),i=1,2,\cdots,n$， $\sum _{i=1}^n{X}_i\sim N(\sum _{i=1}^n{\mu }_1,\sum _{i=1}^n{\sigma }_i^2)$$\sum_{i=1}^n X_i\sim N(\sum_{i=1}^n\mu_1,\sum_{i=1}^n\sigma_i^2)$

还可以进一步推广：有限个相互独立的正态变量的线性组合仍然服从正态分布

0x01 $Z=\frac{X}{Y}$$Z=\cfrac XY$ 的分布、$Z=XY$$Z=XY$ 的分布

设 $(X,Y)$$(X,Y)$ 是二维连续型随机变量，具有概率密度 $f(x,y)$$f(x,y)$，则 $Z=\frac{Y}{X},Z=XY$$Z=\cfrac YX,Z=XY$ 仍为连续型随机变量，其概率密度分别为：

0x02 $M=max\{X,Y\},N=\{X,Y\}$$M=\max\{X,Y\},N=\{X,Y\}$ 的分布

设 $X,Y$$X,Y$ 是两个相互独立的随机变量，其分布函数分别为 $F_X(x),F_Y(y)$$F_X(x),F_Y(y)$

$M=max\{X,Y\}$$M=\max\{X,Y\}$ 的分布函数为：

$N=min\{X,Y\}$$N=\min\{X,Y\}$ 的分布函数为：

也可以推广到有 $n$$n$ 个相互独立的随机变量 $X_1,X_2,\cdots ,X_n$$X_1,X_2,\cdots,X_n$ 的情况，设它们的分布函数分别为 $F_{X_i}(x_i),i=1,2,\cdots ,n$$F_{X_i}(x_i),i=1,2,\cdots,n$，设 $M=max\{X_1,X_2,\cdots ,X_n\},N=min\{X_1,X_2,\cdots ,X_n\}$$M=\max\{X_1,X_2,\cdots,X_n\},N=\min\{X_1,X_2,\cdots,X_n\}$，则它们的分布函数分别为：

常用二维随机变量的分布

考纲摘要：掌握二维均匀分布，了解二维正态分布 $N({\mu }_1,{\mu }_2,{\sigma }_1^2,{\sigma }_2^2,\rho )$$N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)$ 的概率密度，理解其中参数的概率意义

0x00 二维均匀分布

设 $G$$G$ 是平面上的有界区域，其面积为 $A$$A$，若二维随机变量 $(X,Y)$$(X,Y)$ 具有概率密度

则称 $(X,Y)$$(X,Y)$ 在 $G$$G$ 上服从均匀分布

0x01 二维正态分布 $N({\mu }_1,{\mu }_2,{\sigma }_1^2,{\sigma }_2^2,\rho )$$N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)$

二维正态分布 $N({\mu }_1,{\mu }_2,{\sigma }_1^2,{\sigma }_2^2,\rho )$$N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)$ 的概率密度函数为：

其边缘概率密度为：

显然，$X,Y$$X,Y$ 的边缘密度就是 $N({\mu }_1,{\sigma }_1^2),N({\mu }_2,{\sigma }_2^2)$$N(\mu_1,\sigma_1^2),N(\mu_2,\sigma_2^2)$

又有：

显然，$\rho =0$$\rho=0$ 时，$f(x,y)=f_X(x)f_Y(y)$$f(x,y)=f_X(x)f_Y(y)$，这是二维正态随机变量 $X,Y$$X,Y$ 相互独立的充要条件